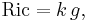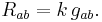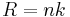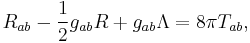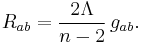Einstein manifold

In differential geometry and mathematical physics, an Einstein manifold is a Riemannian or pseudo-Riemannian manifold whose Ricci tensor is proportional to the metric. They are named after Albert Einstein because this condition is equivalent to saying that the metric is a solution of the vacuum Einstein equations (with cosmological constant), although the dimension, as well as the signature, of the metric can be arbitrary, unlike the four-dimensional Lorentzian manifolds usually studied in general relativity.

If M is the underlying n-dimensional manifold and g is its metric tensor the Einstein condition means that

\mathrm{Ric} = k\,g,

for some constant k, where Ric denotes the Ricci tensor of g. Einstein manifolds with k = 0 are called Ricci-flat manifolds.

Contents

The Einstein condition and Einstein's equation

In local coordinates the condition that (M, g) be an Einstein manifold is simply

R_{ab} = k\,g_{ab}.

Taking the trace of both sides reveals that the constant of proportionality k for Einstein manifolds is related to the scalar curvature R by

R = nk\,

where n is the dimension of M.

In general relativity, Einstein's equation with a cosmological constant Λ is

R_{ab} - \frac{1}{2}g_{ab}R %2B g_{ab}\Lambda = 8\pi T_{ab},

written in geometrized units with G = c = 1. The stress-energy tensor Tab gives the matter and energy content of the underlying spacetime. In a vacuum (a region of spacetime with no matter) Tab = 0, and one can rewrite the Einstein's equation in the form (assuming n > 2):

R_{ab} = \frac{2\Lambda}{n-2}\,g_{ab}.

Therefore, vacuum solutions of Einstein's equation are (Lorentzian) Einstein manifolds with k proportional to the cosmological constant.

Examples

Simple examples of Einstein manifolds include:

Among closed, oriented, 4-manifolds, only those that satisfy the Hitchin–Thorpe inequality can be Einstein manifolds.

Applications

Four dimensional Riemannian Einstein manifolds are also important in mathematical physics as gravitational instantons in quantum theories of gravity. The term "gravitational instanton" is usually used restricted to Einstein 4-manifolds whose Weyl tensor is self-dual, and it is usually assumed that metric is asymptotic to the standard metric of Euclidean 4-space (and are therefore complete but non-compact). In differential geometry, self-dual Einstein 4-manifolds are also known as (4-dimensional) hyperkähler manifolds in the Ricci-flat case, and quaternion Kähler manifolds otherwise.

Higher dimensional Lorentzian Einstein manifolds are used in modern theories of gravity, such as string theory, M-theory and supergravity. Hyperkähler and quaternion Kähler manifolds (which are special kinds of Einstein manifolds) also have applications in physics as target spaces for nonlinear σ-models with supersymmetry.

Compact Einstein manifolds have been much studied in differential geometry, and many examples are known, although constructing them is often challenging. Compact Ricci-flat manifolds are particularly difficult to find: in the monograph on the subject by the pseudonymous author Arthur Besse, readers are offered a meal in a starred restaurant in exchange for a new example.

References